[past] SeLo: Sets and Logic

Our Teaching Page has important information for my students. (It has the Notes, Exams and Links from all of my previous courses.)
The Teaching Page has my schedule, LOR guidelines, and Usually Useful Pamphlets. One of them is the Further information is at our class-archive URL (I email this private URL directly to students).

Assignment for first week of SeLo: (See below, for the materials referred to.)

To help you self-evaluate, take 90 minutes to solve as many problem as you can, on this test of high-school mathematics, with a touch of calculus.
Memorize! the Math-Greek alphabet (pdf).
Work through BoP, sections 1.1 through 1.9. Write-up (but do not hand-in) at least 3 HW problems from pages 1-14.
Read w:Set-builder notation (up through “Equivalent predicates...”), becoming comfortable with the notation.
In PList:, read pages 1-6, memorize abbreviations in Appendix: Notation.
Exams from previous SeLo incarnations:
This will help you decide if my teaching-style is the right style for you.
In SaP (Structure and Proof) work through pages 11-17.
Important: For us, the (double-bar N) symbol ℕ={0,1,2,...}; i.e zero is a natural number, a natnum. This is also the convention in SaP but, unfortunately, not the convention in BoP.
So when you read ℕ in BoP, replace it with ℤ₊={1,2,3,4,...}; the set of positive integers; the posints.

SeLo Resources

Memorize! the Math-Greek alphabet (pdf).
The PList: (Problem List for SeLo has hyperlinks in the Table-of-Contents and the Index.) [Date].
Does Zero = One? (pdf). Here are some ~~proofs~~ poofs about which you can post to our Archive.
Look Ma! All 0 SeLo quizzes so far (pdf) [Date]
Optional: Practice: Binomials, complex arithmetic.
Current: Please work-through w:Euclidean algorithm (up through “Extended Euclidean...” but skip the proofs) and work-through w:Modular arithmetic (through “Applications”).

The Euclidean algorithm can be conveniently applied in table-form; I call this form “Lightning Bolt ” because the update-rule looks like a lightning-bolt (used thrice). Please read the Lightning-bolt algorithm (pdf), learning the algorithm, but skipping the proofs.
Suggestion: Print out on paper (yes, actual paper), the practice sheet for LBolt (pdf) and fill-in the tables.
Current: The first page of Algorithms in Number Theory (pdf), uses LBolt iteratively to compute the GCD of a list of integers, together with its list of Bézout multipliers. Page 2 uses LBolt to solve linear congruences: Find all x where 33x is mod-114 congruent to 18.
Optional: Examples of fusing congruences (txt) using LBolt.
Everybody loves the Euler-Fermat thm. Available is Using EFT to solve 102⁷⁰ + 1 =113= b³⁷ (txt), from Prof. William Stein's book.
Current: A std proof of the Inclusion-Exclusion principle (pdf), together with Candy-Store, Derangement and Stirling-number examples.
An Introduction to Isomorphism, via Gambling. It asks: Why 2, when 76 seems correct?
What is Hall's Marriage (Matching) Lemma?
Future: Our Primer on cardinality.
In addition to proof by raster scan, we can prove that NxN is equinumerous with N via w:Boustrophedon, which can even be pronounced!
Optional: Our Primer on Polynomials has further information on Algebraic Numbers, for the Curious Ambitious Student.
Future, optional: Number Theory grab-bag (pdf). (I wrote this for a NT class, so we'll need to skip parts.) Optional: A proof of the Chinese Remainder Theorem (pdf) [CRT], as a ring-isomorphism thm. Proves that Euler phi is a multiplicative fnc. An example of using CRT to count roots of a polynomial
2022g SeLo syllabus.

Autumn 2023, SeLo:

Aut2023: MHF3202 139A (16397) Sets.&.Logic MWF4[10:40-11:30]
Fine Arts Building 105

The various Math czars who help out.

Computer&Projector	Time	Memory/Telepathy	Whiteboard	CP-Probs
Matthew M.	Olivia	Faythe	everybody	Nick

Look Sis! All 15 SeLo quizzes (pdf).
The cool Home-A preceded the nifty Class-A.
The joyful Home-B for all you Solving Sleuths.

It was followed by the cheerful Class-B.
Our Class-C is now online.

End-of-semester SeLo (Individual Optional Project) IOP-D (pdf)

...was due, slid u n d e r room 402 Little Hall my office door (Little Hall 402, Northeast corner) , no later than 2PM, Thurs, 07Dec2023.

Autumn 2022, SeLo:

Aut2022: MHF3202 139A (16397) Sets.&.Logic MWF5[11:45-12:35]
Fine Arts Building 105

End-of-Semester Games Party 2022t (click for larger)

The various Math czars who help out.

Computer&Projector	CP-Probs	Time	Memory/Telepathy	Whiteboard
Brandon	Alexa & Diego	everyone	Anneka	everyone

Look Ma! All 11 SeLo quizzes (pdf) [Monday, 05Dec2022]
The delightful Home-A.
Typed and well-stapled, your team's write-up was due [with all team-members present] at beginning-of-class on [ ~~Wedn., 28Sep~~ UF closed by hurricane Ian] Monday, 03Oct.
It's first page is the printed problem-sheet, with the blanks filled-in (handwritten is fine).
The heart-warming Class-A was moved to Monday, 03Oct due to hurricane Ian.
For a deeper understanding of iterated LBolt, a 3D integer-lattice is convenient.
Related to the essay question is whether Tilable Union Untilable can be tilable.
Our dodecahedral Home-B was followed by the nicely well-ordered Class-B.
Our bijective Class-C.
2022t Selo syllabus.

End-of-semester SeLo (Individual Optional Project) IOP-D (pdf)

...was due 2PM, Friday, 09Dec2022

Autumn 2021, SeLo:

The spiffy The tilable Class-A (pdf) was enjoyed by all.
Our Home-A (PDF) was due date Wednesday, 20Oct2021.
Home-B (PDF), done individually, was due Monday, 29Nov2021
An intro to the Chromatic polynomial of a graph (pdf); a graphical example of deletion-contraction.
The challenging Individual Project C was due the Thursday after the last day of class.
2021t Selo syllabus.

The Spring 2021, SeLo, page:

Folks appreciated that our first Enjoyable quiz A had no essay question. [Future quizzes will have proofs on them, and students will need to upload a (typically, small) essay as a PDF.]
Scholars showered the keyboard with roses, admiring the Pleasant quiz B with its elegant PHP proof.
SeLoCitizens were entertained by Goofy quiz C starting off with a binomial-identity, and finishing with a nice Induction proof. Cognoscenti cheerfully garnered CP-points by posting solutions (not just answers) to our SeLo Archive.
Cognoscenti marveled at the straightforward induction proof on Daffy quiz D.
Elegant E was everyone's favorite, as it answered that burning light bulb question...
Computer-generated Lmino tiling appear in Pictures of Lmino Tilings (txt). The pictures start about a third of the way down the file. [The top of the file just comprises notes to me, on how to use the code.]

zoid-proofs using induction

The popular Quiz Fantabulous! was a nice productive way end our pandemic Zoomester.
SeLo syllabus

Autumn 2020, SeLo, page, for two online (due to COVID) sections:

Beautifully designed [but unexpectedly eventful due to my unfamiliarity with Canvas], our Exam-A (PDF).
The engaging Exam-B (PDF) went smoothly.
The Individual End-of-Semester Project was administered via Canvas.
The 2020t Selo syllabus.

The Spring 2020, SeLo, page:

Our Class-A and Home-A were entertaining.
The interesting IP-B (Individual-Project B), folks told me, was challenging.
All B-teams have emailed me their Home-B. Thank you.
Look Pa! All 5 SeLo quizzes (pdf).
Our SeLo syllabus (txt) has clickable links.

End-of-semester SeLo Individual Project D (IP-D)

[Problems (D2(C)) and (D3) are challenging. Don't delay, said the Wise Person...] Prof.

...was due, emailed to me, squashATuflDOTedu, as a PDF! no later than 5PM, Tuesday, 28Apr2020.

The SeLo Project must be carefully typed, but diagrams may be hand-drawn and scanned into the PDF.

The various SeLo czars who helped:

Time	Computer	Memory/telepathy	Spur-OTM-Probs	Phone
Jonathan S.	Teegan B.	Yasmeen G.	Blake W.	Chris P.

Autumn 2019, SeLo:

In one convenient location: All 9 SeLo quizzes (pdf),
The Lminoish Class-U
Our Home-U had solns. Related to the exam are Pictures of Lmino Tilings (txt), to illustrate a geometric induction-argument.
Our Home-V.
Essay (V3) had you label the vertices a dodecahedron. You may have found it convenient to print out the edge-graph of a dodecahedron for your vertex-label diagrams.

Available is a template, for folding-together a 3D-dodecahedron.
The bijective Class-W.
The intriguing IOP-X had a Pigeon-hole Principle question, and a cardinality question.
Our SeLo syllabus/calendar.

The various Math czars who help out:

Time	Computer	Memory/telepathy	Blackboard	Spur-OTM-Probs
Chase	Atharva	Sienna	Nathan	Bhaskar

Autumn 2018, SeLo:

Our textbook is How to prove it, (Second Edition).

Author:	Daniel J. Velleman	ISBN-13:	978-0521675994
Year:	2006	Publisher:	Cambridge University Press

Here are links to this book at The Publisher's site and at Amazon.com.

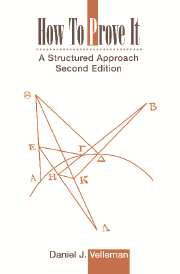
SeLoidal czars who aided the course:

Time	Computer	Spur-OTM-Probs	Phone-list
Kailey S.	Jeremy M.	Joey, Mario, Patrick	Aerin B.

In one convenient location: All 9 SeLo quizzes (pdf).
The cute Home-A was followed by the highly-praised Class-A, much admired for its two-tone format, and the comic relief of the Three Stooges.
Tilable Home-B (pdf) was loads of fun.
Computer-generated pictures of Lmino Tilings (txt), illustrating a geometric induction-argument.

The domino-tiling sequence on 2xN leads to the roots of the problem.

The nifty Class-B graced its way into existence on Wedn., 24Oct2018.
We went One-on-One with the cheery Class-C, and we Won!
The dodecahedral IOP-D needed several pictures.
Voila! our SeLo syllabus.

Part of the Spring 2017 SeLo page:

End-of-Semester Games Party (click for larger)

Math czars:

Time	Computer	Blackboard	Spur-Probs	Phone-list
Leah	Leah	Christopher P.	Nicholas C.	Lizzie(Donna)

Our end-of-semester extra topic was: Introduction to the Chromatic polynomial of a graph (pdf).
Available are all the SeLo quizzes so far (pdf).
The thought-provoking Home-V also provoked great joy, with its three interesting essay questions.
This was followed by the cute Class-V.
The multi-dimensional Home-W, nicknamed Waldo inspired greatness.
Folks thrilled to Class-W and its comforting question about Lminos, with which the cognoscenti were already familiar.
[29Mar2017]: Applause showered Class-X [the last in-class exam of the semester, people tearfully observed], with its Nifty use of Schroeder-Bernstein, to prove a surprising result about the set of continuous functions.
The SeLo syllabus, with dates is available.
The intriguing IOP-Y was due 2PM, Thursday, 20Apr2017

Voila! some of the Spring 2015, SeLo, page:

Our syllabus gave an overview.
Our exams were:

Team W-home and individual W-class, the in-class component.
Team X-home and individual X-class.
In-class Y-class; there was no team component.
Finally, there was an Individual Optional Project IOP-Z at semester's end.

Useful info from the Spring 2014, SeLo, page:

We had a test of prerequisites as well as four microquizzes during the semester.
The exams were:

Team W-home and individual W-class.
Team X-home and individual X-class.
At semester's end, there was the Optional IOP-Y which had you do a Schroeder-Bernstein computation.

A section of the the Autumn 2013 SeLo page:

Available are all the SeLo quizzes (pdf).
Cheering crowds greeted the Gregorianish Class-U (pdf) with its 2-term linear recurrence and correct spelling of February! Folks rushed to post solutions for their colleagues to admire.
The delightful Home-V (pdf) was available early, for your team to solve. Home-V was due at the BoC [Beginning Of Class] on Monday, 21Oct.
The cheerful individual component, Class-V (pdf) [Wedn., 23Oct.] was well-received by the Mathematical Intelligentsia, appreciating its tight connection to Home-V.
Insightful, engaging, absorbing Home-W (pdf) became available the evening of Tuesday, 12Nov.. It was due at the BoC on Monday, 18Nov..
Class-W (pdf) the individual component, revealed itself on Wednesday, 20Nov..
Cardinaltiy arguments were cental to IOP-X [noon, Monday, 09Dec2013.]
SeLo syllabus (txt).

Helpful Math czars.

Time	Computer	Chalk	ES-Probs	Phone-list
Rico	Corey	Sam-C	Alex	David

Part of the Spring 2012 SeLo page:

The various Math czars who help out:

Time	Computer	Chalk	Blackboard	ES-Probs	Phone-list
Annie	Sofia	Stewart	Ian	Christopher M.	Alejandra

SeLo quizzes 2012g (pdf).
The magical Home-W (pdf) challenged your team's gray-cells with modular arithmetic. The take-home was due at BoC, on Monday, 06Feb2012. It nicely foreshadowed the Class-W (pdf), eliciting shouts of enthusiasm.
Inspired by Class-X (pdf), the crowd cried Give us more Zinc, Tin, Silver and Gold! —5 atoms; that's just not enough! All this followed the nifty Home-X (pdf), which was due by noon, on Tuesday, 28Feb2012, slid completely under my office door.
Folks found that Class-Y (pdf), was well-Suited to their bijective knowledge.
Our IOP-Z had had an affine-code that students needed to decode!
Voila: A printable SeLo syllabus. Here is our schedule.

Part of the Spring 2011 SeLo page:

Classroom czars who helped out:

ES-Probs	Computer	Time	Chalk	Blackboard	Phone-list
Mallory	Corey	David S.	Esther	Kristen	Blanko

(∃ another photo at bottom of page)

Available are all the quizzes so far (pdf).
Prior to the prereq Class-T, you looked at the sample test (pdf).
The highly-anticipated and outrageously upbeat Class-U, entranced the cognoscenti with its cute use of the Gregorian calendar, and its nifty induction proof. While a few carped that it was “Too easy!”, the general population raved about the exam's clean lines and minimalistic two-tone format. Critics were unanimous in their praise of questions that were slight alterations of earlier quiz and class conundra. A Smash Hit!, concluded all the major newpapers... and crys of “Encore!” and “Author! Author!” echoed throughout the Realm.
N travelers peregrenated through Class-V (Wed., 2Nov.), discovering that, starting at any question, they could visit all the questions.
Better than getting bitten by a rabid squirrel!, was the general consensis. (A minority opined Comparable to rabid-squirrel bites —but with less fur...)
We liked Class-W so much, that we decided to spend an extra half-hour with it. Now that is one popular exam! (Taken, on Friday, 18Nov).

Here is part of the Autumn 2009 SeLo page:

The various Math czars who helped out:

Computer	Time	Phone-list	Chalk
Marc	Sigrun	Cara	John

Individual-Project Home-E was due 1PM, Friday, 11Dec2009, carefully typed, but diagrams may be hand-drawn.
Quizzes so far, and potential problems (pdf).
Week-15: Mon, Wed (7 and 9 Dec) are the last two days of class. Schroeder-Bernstein theorem.
Week-14: Divisibility. Cardinality of sets, Cantor's diagonal argument. Project Home-E available Friday, 04Dec.
Week-13: Monday: Further discussion of divisibility, and how the Euclidean algorithm applies to polynomials. (Wed, canceled; Fri is Thanksgiving vacation).
Week-12:
The fascinating SeLo-D (pdf) got rave reviews; the Crowd Clamored for More! [Wed, 18Nov.]

Some examples of computer generated Lmino tilings (txt).
Week-11: Examples of induction: Fibonacci numbers, and 2 base cases. Every posint factors as a product of primes irreducibles (existence). All horses have the some color. Lmino tiling.
Week-10: Defns of a lattice, a particular kind of poset (partially-ordered set). Strong/weak induction. Non-constructive proof: There exists positive irrational numbers B,E such that B^E is rational.
Week-9: Read 4.3.
We had the stimulating SeLo-C (pdf) in class on Wed, 28Oct.

Hopefully, Eager Mathematicians rush to post Solutions….
Week-8: Vacuous operations. What means the empty sum, empty product empty max empty gcd?
Week-7: Please finish reading sections 3.1–3.7. For 26Oct, have read 4.1, 4.2.
Indexed and non-indexed big-operators.

Decimal notation and repeated decimals .

Binomial and multinomial coeffs. Proof of Fermat's Little Thm by induction. Using a binomial coeff to count the number of ways of choosing N objects out of T distinguished types.

There was a makeup SeLo-B (pdf) for those with a legitimate reason for missing the original; please post solns.
Week-6: We continue in chapter 3. On Mon, 5Oct, we had extra classes, 9^th&10^th periods, in LIT127. We had our thought-provoking SeLo-B (pdf) on Wed, 7Oct., and here is a write-up of the congruence proof (pdf).
Week-5: More on quantification. Introduced the Powerset operator. Please finish reading chapter 2 by Friday, 2 Oct.
Week-4: Please cogitate deeply over iterated LBolt & linear congruences (pdf).
We: Started Quantifiers and reviewed Free variables and these functions: d(), sigma(), EulerPhi(), floor(), ceiling(). Discussed notations for tuples/sequences, gcd of tuple or set, relation between contrapositive, converse and inverse of a stmt.
Week-3:
We start Propositional logic (also called sentential logic ). Play with the Venn-diagram self test, noting that this page uses B' to mean the complement of B, which we generally write a B^c. [ASIDE: Please read our general terminology (pdf).]

We'll also look at the w:Euclidean Algorithm (i.e, the Lightning Bolt algorithm). The LBolt frame (pdf) has seven practice problems on page 1 [LBolt answers (txt) are available], and six make your own problem on page 2.

Please grok completely how to easily solve a linear congruence (pdf).
Week-2: Please print and read Mersenne primes and Even Perfect numbers (pdf).
We proved that Primes has arbitrarily long gaps. We proved Euclid's thm that there are infinitely many primes.

Having defined the arithmetic progression AP(s,G) := [s + GZ], we stated Dirichlet's thm for coprime APs. We noticed that Euclid's thm is the special case AP(0,1) of Dirichlet's. We proved Dirichlet's for AP(-1,4), and Prof. King gave an exercise to prove the same for AP(-1,3), and AP(-1,6).

We defined w:Modular arithmetic and proved that addition/subtraction and multiplication are preserved, mod N.
Week-1: Primes and Mersenne primes and w:Perfect numbers.
Week-0:
David Gale's Game of chomp in w:Wikipedia. Doron Zeilberger's Three-rowed Chomp.

John posted some solns to our prerequisite mini-exam SeLo-A (pdf).

Please take a gander at our Syllabus (txt) and Past courses with notes, exams and links.

Material from the Spring 2008 SeLo page:

Our textbook was Sets, Functions and Logic (Third Edition).

Author:	Keith Devlin	ISBN:	978-1584884491
Year:	2003	Publisher:	Chapman & Hall/CRC

The Math czars who helped out.

E-Probs	Computer	Phone-list	Chalk	Blackboard	Time
Karly & Josh	Michael	Kyle	Vincent	Ben	Ross

Applause and acclaim was the response to the gorgeous Prereq-A (pdf) with its clean lines, and minimalistic two-tone format; this was the test of prerequisite knowledge.
General gaity greeted the taut Class-B (pdf) with its reference to Lewis Carroll and its nice mix of problems.
Here is the practice exam for Class-C (pdf), together with the actual Class-C (pdf). Rumor has it that this exam was the right length :-)
Many folk finished Class-D (pdf) early, so as to go home and read about Completeness in Chapter 5. I invite you to post solutions to our archive.

Voila a practice exam for Class-D (pdf). It is quite similar to, but longer, the actual Class-D.
Individual final-project E (pdf), was due, 2PM, Friday, 25Apr2008, carefully typed.

Sets and Logic

SeLo Resources

Web resources

Tips on writing proofs

Ending in style

End-of-semester SeLo (Individual Optional Project) IOP-D (pdf)

End-of-semester SeLo (Individual Optional Project) IOP-D (pdf)

End-of-semester SeLo Individual Project D (IP-D)